Initiation au jeu de Nim

J’ai envie de débuter une série d’articles sur la théorie des jeux. C’est un domaine particulièrement intéressant des mathématiques et surement un des plus ludiques. Je vous propose de démarrer par une catégorie extrêmement simple de jeux qu’on appelle couramment les jeux de Nim.

Pour ceux qui l’ignorent, les jeux de Nim sont une catégorie de jeux où deux joueurs s’affrontent au tour par tour et qui consistent à prendre ou déplacer des objets en respectant certaines règles pour passer d’un état à un autre (sans avoir la capacité de revenir à un état précédent) jusqu’à atteindre une position de victoire. Cela a l’air assez flou comme ça, n’est-ce pas ? C’est normal, c’est une définition générique car les jeux de Nim englobent un nombre de jeux assez large même si derrière, il y a toujours la même logique. Un des jeux de Nim les plus connus a été rendu populaire à notre époque par une épreuve de Fort Boyard, celle des bâtonnets. Deux joueurs ont devant eux un plateau où se tient un certain nombre de bâtonnets. À chaque tour, le joueur a la capacité de retirer un, deux ou trois bâtonnets. Celui qui retire le dernier bâtonnet a perdu. Ceci est un jeu de Nim, on a deux joueurs qui alternent, chacun peut retirer un certain nombre d’objets fixé par les règles initiales et on arrive à une situation finale qui est de vider le plateau tout en sachant que celui qui prend le dernier perd. En outre, il est impossible de retourner à un état précédent car on ne peut que retirer des bâtonnets. À l’inverse, les échecs par exemple ne sont pas un jeu de Nim car on peut totalement revenir à une position antécédente. Par exemple, je bouge mon cavalier, mon adversaire fait de même puis je remets mon cavalier à sa place initiale et mon adversaire fait de même. Ici, on vient de passer d’un état de l’échiquier à un autre strictement identique. Cela signifie que tout ce qu’on va voir pour être sûr de gagner dans un jeu de Nim ne peut pas s’appliquer dans un jeu d’échec.

Je me dois également de préciser certaines caractéristiques inhérentes au jeu de Nim. Il n’y a pas, dans un jeu de Nim, de notion de hasard. Si je prends l’ensemble des jeux avec des dés par exemple, tel que les petits chevaux, ce ne sont pas des jeux de Nim. C’est également un jeu qui se doit d’avoir ce qu’on appelle des informations complètes et parfaites. Cela signifie qu’on connait exactement l’ensemble des variables qui constituent le jeu. Dans mon jeu des bâtonnets, je vois combien de bâtonnets au total et je sais combien moi et mon adversaire avons la capacité de retirer. À l’inverse, la plupart des jeux de cartes ne sont pas des jeux de Nim tel que le Black Jack ou le Poker car nos informations ne sont pas complètes et parfaites tant on ignore la main de nos adversaires. Là encore, pour ces jeux, c’est d’autres stratégies qu’il va falloir adopter que celle du jeu de Nim. Enfin, un jeu de Nim est un jeu à somme nulle. Cela signifie que si je gagne une manche alors l’autre joueur en perd obligatoire une. Il n’y pas de situations où tout le monde est vainqueur ou perdant. Vous notez que tout ça est assez restrictif mais c’est normal, on a dit qu’on commençait simple. On ne va pas se lancer dans des probabilités ou des graphes à circuits.

Dans tout jeu de Nim, la stratégie est la suivante. La phase la plus complexe est la première, il va falloir lister l’ensemble de tous les états possibles du jeu. En un sens, ce n’est pas difficile, c’est juste long et rébarbatif. Après, on a des ordinateurs pour faire ça maintenant. Ensuite, on tisse les liens qui, en fonction des règles, nous permette de passer d’un état à l’autre. Imaginons dans notre jeu des bâtonnets (qui se fait très bien avec des allumettes aussi), on commence avec 12 éléments alignés. On a donc une liste décroissante de 12 à 1 et comme on peut retirer un, deux ou trois à chaque tour, alors chaque élément est lié à son élément-1, élément-2 et élément-3. Cela nous donne le graphe orienté suivant :

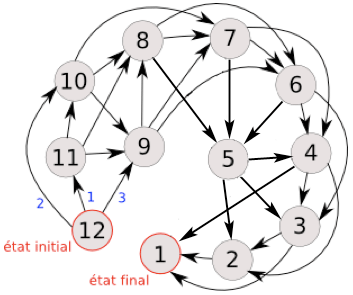
Une fois le graphe fait, vous venez de faire le plus dur du travail. Maintenant, il faut déterminer les états finaux. Dans le cas de notre jeu de bâtonnets, il n’y en a qu’un. C’est quand il en reste plus qu’un. En effet, si on arrive à la fin de notre tour au cas où il n’en reste plus qu’un, on a gagné car l’autre n’a d’autre choix que de le retirer. Mais dans d’autres jeux de Nim, il peut y avoir plusieurs états gagnants. Le but est de les répertorier. À partir de là, on va voir tous les états qui pointent sur eux. Dans notre cas, par exemple, on a le 2, 3 et 4. Ces cas sont considérés comme perdants. Pourquoi ? Car si à la fin de votre tour, vous atterrissez sur un de ces états, votre adversaire peut atteindre la position gagnante et donc vous perdez. On ne veut pas ça. Par contre, c’est tout le sort qu’on souhaite à notre adversaire. C’est pour ça que nous allons chercher un état qui ne mène qu’à des états perdants. Est-ce qu’on a cela ? 5 mène à 2, 3 et 4 qui sont tous perdants. Ainsi, si j’arrivais sur 5, mon adversaire n’aurait d’autres possibilités que de venir sur un état perdant. On dit que 5 est un état gagnant. Et comme 5 est un état gagnant, on reproduit le même processus qu’avec 1. Les états qui pointent dessus sont déclarés perdants et on cherche un état qui pointe que sur des perdants. Il devient un nouveau gagnant et on continue jusqu’à arriver à l’état initial. Ces éléments gagnant sont appelés noyaux. Dans notre cas, on arrive au résultat suivant :

Comme notre logique est bien faite, on note que les éléments du noyau peuvent être tous atteint en deux tours. C’est trivial vu que les perdants pointent forcément sur un gagnant et qu’un gagnant ne pointe que sur des perdants. Ainsi, si à la fin de votre tour, vous arrivez sur une situation gagnante, alors vous êtes sûr de gagner si vous jouez bien. Votre adversaire n’ayant pas le choix de tomber sur un cas perdant, vous devrez alors rejoindre le prochain cas gagnant. Si votre êtes sur 9 et que votre adversaire en retire 3 et atterrit donc sur 6, n’allez pas sur 4 mais sur 5. De même, si vous commencez, allez vite en 9 en en retirant 3.

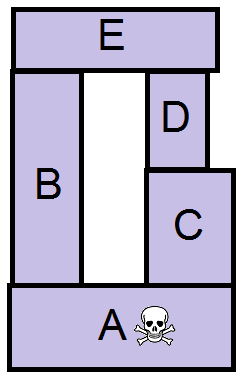
Ainsi, les jeux de Nim ne sont guère intéressants si on joue avec des personnes éclairées car dès le début, vous pouvez savoir qui a gagné ou perdu. Je prends par exemple, le morpion ou tic-tac-toe, je pense qu’on y a tous joué étant enfant. Une fois qu’on sait bien y jouer, au bout du second coup, on sait si on gagne ou si on fait un match nul (si le joueur joue bien, car sinon, il peut commettre des erreurs et on peut les exploiter pour gagner). Après, bien que déterminable, on ne s’amuse pas toujours à calculer les noyaux d’un graphe dans notre tête. Car créer le graphe peut s’avérer parfois complexe bien que possible. Par exemple, si je prends le puissance 4, le nombre de configuration possible est énorme. Mais on peut le faire (ce qui me permet de vous dire que si deux joueurs jouent parfaitement au puissance 4, si le premier joueur met son pion au milieu, il est assuré de gagner et à l'inverse s'il le met sur les extrémités, il est assuré de perdre). Malgré tout, sur les Nim, cette stratégie marche toujours. Je vous laisse l’essayer sur ce petit jeu. Vous et votre adversaire vous retrouvez devant cette pile. À chaque tour, vous devez retirer un morceau. Attention toutefois, Si vous prenez une pièce, vous êtes obligé de prendre toutes les pièces qui sont au-dessus de celle-ci. Celui qui prend le dernier morceau avec le crane a perdu. Vous débutez, quelle pièce devez-vous prendre ?