Aller plus loin avec les intégrales

Vous venez de finir votre terminale scientifique et vous voulez aller plus loin avec les intégrales que ce que vous avez vu jusqu'à lors. Ou vous êtes tout simplement un fan de mathématique qui souhaite découvrir d'autres manières de résoudre des intégrales.
Je vous souhaite la bienvenue dans cet article qui a justement pour but de vous faire découvrir ou redécouvrir des éléments passionnants sur les intégrales.

Attention néanmoins! Je considère qu'actuellement vous connaissez ce qu'est une intégrale, comment en résoudre une et que vous connaissez vos primitives. Le but de ce tutoriel n'est pas de vous apprendre cela. Si ce n'est pas le cas, je vous conseille de potasser un petit peu les cours sur les intégrales puis de revenir.

Bien, avant de commencer, il serait bon de savoir de quoi on parle, n'est-ce pas?

On a du vous dire que l'intégrale d'une fonction positive sur les bornes de l'intégrale était l'aire comprise entre la courbe représentative de la fonction, l'axe des abscisses et deux droites de type [math]x= c , c\in \mathbb{R}[/math].
À l'inverse, l'intégrale d'une fonction négative sur les bornes de l'intégrale était l'opposé de l'aire comprise entre la courbe représentative de la fonction, l'axe des abscisses et deux droites de type [math]x= c , c\in \mathbb{R}[/math].

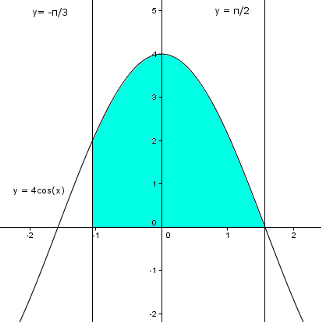
Autrement dit: [math]\int_{-\frac{\pi}{3}}^{\frac{\pi}{2}} {4cos(x) dx}[/math] est l'aire comprise entre la courbe de la fonction 4cos(x), l'axe des abscisses et les droites [math]x=-\frac{\pi}{3}[/math] et [math]x=\frac{\pi}{2}[/math] car 4cos(x) est positif sur [math][-\frac{\pi}{3};\frac{\pi}{2}][/math]
Ce qui nous donne graphiquement l'aire coloriée en bleu:

Si tout le monde est d'accord, on peut continuer. On a dû vous apprendre également qu'une intégrale d'une fonction est la différence entre deux primitives de cette même fonction. C'est-à-dire, soit f, une fonction quelconque, et F, une des primitives de f, alors:
[math]\int_{a}^{b} {f(x)} = F(b) - F(a)[/math]

Alors voilà ma grande question, en quoi une différence de primitives définit-elle une aire?

Pour comprendre, je vous invite à voir ce schémas (c'est un schémas, on ne cherche pas la qualité artistique ):

Bon je vais l'expliquer un peu. On a une fonction f. On a également une fonction A(x) qui calcule l'aire qu'il y a entre la courbe représentative de la fonction f, l'axe des abscisses, la droite d'équation x=a et une autre borne (comprit entre a et b) qui est d'abscisse x. Ainsi l'aire hachurée en rouge est A(x), l'aire au fond bleu est A(x+h) avec h, un réel quelconque et l'aire hachurée en vert, c'est A(x+h)-A(x).

Attend! Ton aire hachurée en vert dépasse, elle forme un rectangle dont un bout est au dessus de la courbe de la fonction.

Je sais et c'est fait exprès. Le fait est que plus h est petit, plus on se rapproche de l'aire réelle de A(x+h)-A(x).
Donc pour le moment, posons cette approximation, A(x+h) - A(x) est l'aire hachurée en vert. Tient mais comme tu l'as fait remarquer, c'est un rectangle. Or nous savons calculer l'aire d'un rectangle. Pour ceux qui ont oublié, l'aire d'un rectangle, c'est longueur x largeur. Ici, la largeur est de h (puisqu'on a décalé de h) et la longueur, c'est quoi? Comme vous le voyez sur le schéma, c'est f(x).
Donc [math]A(x+h) - A(x) \simeq h \times f(x)\Rightarrow \frac{A(x+h) - A(x)}{h} \simeq f(x)[/math]
Comme je le rappelle, plus h est petit, plus on se rapproche de l'aire réelle de A(x+h) - A(x).
Donc [math]\lim_{h \to 0} \frac{A(x+h) - A(x)}{h} = \lim_{h \to 0}f(x)[/math]. Or f ne dépend pas de h donc [math]\lim_{h \to 0}f(x) = f(x)[/math]. Ainsi [math]\lim_{h \to 0} \frac{A(x+h) - A(x)}{h} = f(x)[/math]

Mais là, vous devez remarquer quelque chose...non? À propos d'une dérivée? Et oui, rappelez-vous que [math]\lim_{h \to 0} \frac{A(x+h) - A(x)}{h} = A'(x)[/math]. On obtient donc [math]A'(x) = f(x)[/math]. Ainsi la fonction A serait une primitive de la fonction f.

Maintenant posons F comme une autre primitive de la fonction f. Alors [math]F'(x) = A'(x) = f(x)[/math]. De cela, on est déduit que [math]F'(x) - A'(x) = 0 \Rightarrow (F-A)'(x) = 0 \Rightarrow (F-A)(x) = c , c\in \mathbb{R} \Rightarrow F(x) - A(x) = c[/math]
Or c est une constante, cela signifie que cela vaut pour tout x. Par conséquent c'est valable pour x = a. Donc [math]F(a) - A(a) = c[/math]. Mais A(a) est l'aire qu'il y a entre la courbe de fonction f, l'axe des abscisses et la droite d'équation a et la droite d'équation a... mais l'aire est nulle. Donc A(a) est nulle. On obtient donc [math]F(a) = c[/math]. Tient, mais on l'a trouvé notre constante. Reprenons notre équation: [math]F(x) - A(x) = F(a)[/math].
Et si on prenait désormais x = b. Cela voudrait dire [math]F(b) - A(b) = F(a)\Rightarrow A(b) = F(b) - F(a)[/math].
A(b) est l'aire comprise entre la courbe de f, l'axe des abscisses et la droite d'équation a et la droite d'équation b. Mais c'est l'intégrale de a à b cela.

De cela, on en déduit que [math]\int_{a}^{b} {f(x)dx} = F(b) - F(a)[/math].
Voici comment on explique que la différence de deux primitives soit égale à une aire (ou à son opposé).

On a vu qu'on pouvait faire intervenir la fonction arctan, fonction paire, dans des intégrales. Je vous propose donc de nous intéresser à la résolution d'intégrale avec des fonctions paires ou impaires.

En réalité, cette partie va plus être de l'observation et de la logique qu'un raisonnement mathématique pur et dur. Regardons donc la courbe de notre fonction [math]f(x) = 4cos(x)[/math] qui est paire puisque [math]f(-x) = 4cos(-x) = 4cos(x) = f(x)[/math] et son ensemble de définition est centré en 0.

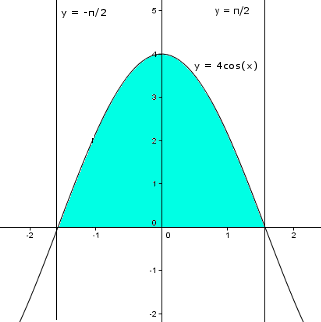
Là, on cherche une nouvelle expression égale à [math]\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} {4cos(x)dx}[/math]. Regardons, l'aire de la zone bleu, on est assez d'accord sur le fait que la zone bleu est symétrique par rapport à l'axe des ordonnées.
De ce fait, [math]\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} {4cos(x)dx} = 2\int_{0}^{\frac{\pi}{2}} {4cos(x)dx}[/math]. Et cela marche pour toutes les fonctions paires à condition que leurs bornes soient symétriques par rapport à 0.

On peut donc généraliser. Pour f, fonction paire, on a [math]\int_{-a}^{a} {f(x)dx} = 2\int_{0}^{a} {f(x)dx}[/math]

Intéressons nous maintenant aux fonctions impaires. Vous allez voir, c'est beaucoup plus rapide. Prenons comme exemple [math]f(x) = 4sin(x)[/math],fonction impaire, car [math]f(-x) = 4sin(-x) = -4sin(x) = -f(x)[/math] et l'ensemble de définition de f est centré en 0. Observons sa courbe représentative est ci-dessous:

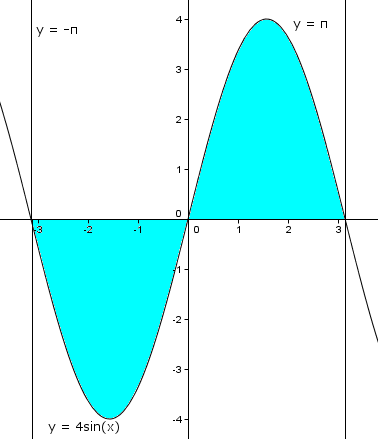
Sur des bornes symétriques par rapport à 0, on est d'accord que l'aire de la zone bleu qui est sous l'axe des abscisses est égal à l'aire de la zone bleu qui est au dessus de l'axe des abscisses. Or l'aire de la zone bleu est justement sous l'axe des abscisses donc c'est l'opposé de l'intégrale de la même zone bleu mais au dessus de l'axe des abscisses. Les deux s'annulent donc. Ainsi [math]\int_{-\pi}^{\pi} {4sin(x)dx} = 0[/math]

On peut généraliser en disant que pour f, fonction impaire, [math]\int_{-a}^{a} {f(x)dx} = 0[/math]

Voilà, c'est tout pour cette partie. Il n'y a pas grand chose à dire mais cela peut vous éviter de faire des calculs très compliqués du style intégration par partie ou par changement de variable.

Il y a certaines intégrales un peu compliquées à résoudre. Pour cela vous avez du voir des techniques telles que l'intégration par partie que je considère comme acquise. Je vous propose de résoudre l'intégrale suivante :
[math]I = \int_{1}^{4} {\frac{1}{1+\sqrt{t}}dt}[/math]
Avec les méthodes actuelles, cela risque d'être compliqué. Pour cela, je vais vous apprendre une nouvelle méthode de résolution, que l'on appelle l'intégration par changement de variable.
Le principe est simple, on change notre variable t par une autre variable afin d'obtenir une forme qui nous arrange plus (comprendre par là, dont on est capable de trouver une primitive). Posons ici: [math]x = \sqrt{t}[/math]. Cela revient à dire que x est le résultat d'une fonction f de paramètre t. Je peux donc mettre [math]x = f(t) = \sqrt{t}[/math]

Super alors maintenant on change notre variable t par notre variable x et on résout.
Désolé mais non! Cela serait trop facile. En effet, un élément dont vous vous êtes surement jamais soucié jusqu'à maintenant entre en ligne de compte. C'est le fameux dt, car effectivement, dt n'est pas toujours égal à dx. Mais comment trouver dt en fonction de dx,alors?
Pour cela, intéressons nous à la dérivé de f(t),c'est-à-dire f'(t). Il y a une autre notation pour exprimer la dérivé d'une variable x par rapport à une autre variable t, une notation plus utilisée en Physique qu'en Mathématique, c'est [math]\frac{dx}{dt}[/math]. Donc [math]\frac{dx}{dt}[/math] est la dérivée de x par rapport à t, autrement dit, c'est f'(t).
Ainsi [math]\frac{dx}{dt} = f'(t) \Rightarrow \frac{dx}{dt} = (\sqrt{t})'\Rightarrow \frac{dx}{dt} = \frac{1}{2\sqrt{t}}[/math]. Or on a dit que [math]x = \sqrt{t}[/math]. D'où [math]\frac{dx}{dt} = \frac{1}{2x}\Rightarrow dt = 2x \times dx[/math]
On a finalement réussit à exprimer dt en fonction de dx. Bravo.

Mais ce n'est pas encore fini. On vient de changer l'expression à intégrer, il est normal que les bornes ne soient plus les mêmes. Pour avoir les nouvelles bornes, il suffit d'appliquer la fonction f ( ici, racine carré ) à nos bornes et puis c'est bon. En conséquence, les nouvelles bornes dans notre exemple sont [math]\sqrt{1} = 1[/math] et [math]\sqrt{4} = 2[/math]

Ainsi [math]I = \int_{1}^{4} {\frac{1}{1+\sqrt{t}}dt} = \int_{1}^{2} {\frac{1}{1+x}\times 2x \times dx}[/math]. On peut sortir 2 qui est une constante multiplicative de l'intégrale. On obtient : [math]2 \times \int_{1}^{2}{\frac{x}{1+x}dx}[/math].
Et ici, il faut penser à une astuce qui est la suivante : [math]x = x +1 - 1[/math].
Ainsi [math]2 \times\int_{1}^{2}{\frac{x+1-1}{1+x}dx} = 2 \times\int_{1}^{2}{\frac{x+1}{1+x} - \frac{1}{1+x} dx} = 2 \times\int_{1}^{2}{1 - \frac{1}{1+x} dx} = 2 \times [x - ln(1+x)]_{1}^{2}[/math]
[math]= 2\times[(2-ln(3))-(1-ln(2))] = 2\times (ln(\frac{2}{3})+1)[/math]

À retenir: on pose notre nouvelle variable x en fonction de l'ancienne t. On cherche ensuite dt en fonction en dx. Enfin on pense à changer les bornes en leur appliquant la fonction. Puis on résout. Vous voyez, l'intégration par changement de variable n'a rien de bien compliqué

Un autre exemple pour terminer cette partie. J'en profite pour vous apprendre (peut-être) la dérivé de arctan : [math](arctan(x))' = \frac{1}{1+x^2}[/math]. Retenez cette dérivé car elle vous sera utile pour l'exemple mais également pour la suite. Bien, résolvons alors :

[math]\int_{-1}^{0} {\frac{1}{t^2+2t+2}dt}[/math]. Le polynôme au dénominateur ressemble presque à une identité remarquable.
[math]\int_{-1}^{0} {\frac{1}{(t^2+2t+1)+1}dt} = \int_{-1}^{0} {\frac{1}{(t+1)^2+1}dt}[/math]. On a presque la dérivé de arctan, faudrait juste changer t+1 en une variable. Alors effectuons une intégration par changement de variable, posons [math]x = t+1[/math]
Pour le coup, on a [math]\frac{dx}{dt} = (t+1)' \Rightarrow \frac{dx}{dt}= 1 \Rightarrow dx = dt[/math]. Et les nouvelles bornes sont 0 et 1 puisqu'on ajoute juste 1. Notre intégrale devient : [math]\int_{0}^{1} {\frac{1}{x^2+1}dx} = [Arctan(x)]_{0}^{1} = Arctan(1) - Arctan(0) = \frac{\pi}{4} [\pi][/math]

En effet, [math]Arctan(0) = 0[/math]. Pour mieux comprendre, il faut trouver l'angle tel que [math]tan(y) = 0 \Rightarrow y = 0[\pi][/math]. De même pour [math]Arctan(1) = \frac{\pi}{4}[/math], il faut résoudre [math]tan(y) = 1 \Rightarrow \frac{sin(y)}{cos(y)} = 1 \Rightarrow sin(y) = cos(y) \Rightarrow y = \frac{\pi}{4} [\pi][/math]

Voilà c'est la fin de ce chapitre sur l'intégration par changement de variable sur cette exemple d'arctan. Vous ne vous attendiez pas à trouver des angles dans un cours sur les intégrales, n'est-ce pas?

Il y a quelques fonctions rationnelles que vous savez intégrer tel que [math]\int_{1}^{e} {\frac{1}{x} dx} = [ln(x)]_{1}^{e} = 1[/math]
Or ceci est une fonction rationnelle particulière. Qu'en est-il si je vous demande de résoudre : [math]\int_{-1}^{0}{\frac{2x+7}{x^2+x-2}} dx[/math].
C'est plus compliqué. Bon, je vais vous apprendre dans cette partie à intégrer une fonction de type : [math]f(x) = \frac{ax+b}{x^2+px+q}, a, b, p, q \in \mathbb{R}[/math].

On note qu'il y a trois cas, un selon la valeur du discriminant. Faisons par disjonction des cas:

Si [math]\Delta > 0[/math]
Si [math]\Delta > 0[/math] alors le polynôme a deux racines que j'appellerais c et d. On peut alors trouver une nouvelle expression de f(x) tel que [math]\frac{ax+b}{x^2+px+q} = \frac{\alpha}{x-c} + \frac{\beta}{x-d}[/math]. On a plus qu'à déterminer [math]\alpha\ et\ \beta[/math]. Ensuite on sait trouver la primitive.

Regardons notre exemple plus haut. [math]\int_{-1}^{0}{\frac{2x+7}{x^2+x-2}} dx[/math]. Ici les racines sont assez évidentes, c'est 1 et -2. Pas la peine de calculer le discriminant et chercher les racines. [math]\frac{\alpha}{x-1} + \frac{\beta}{x+2} = \frac{\alpha\times (x+2) + \beta\times (x-1)}{(x+2)\times (x-1)} = \frac{(\alpha + \beta)x + 2\alpha - \beta}{x^2+x-2}[/math].
Par identification des termes, on a : [math]\left\{\begin{array}{l c r}\alpha + \beta = 2\\2\alpha -\beta = 7 \end{array}\right. \Rightarrow \left\{\begin{array}{l c r}3 \times \alpha = 9\\2\times \alpha - \beta = 7 \end{array}\right. \Rightarrow \left\{\begin{array}{l c r}\alpha = 3\\
\beta = -1 \end{array}\right.[/math].
D'où [math]\int_{-1}^{0}{\frac{2x+1}{x^2+x-2}} dx = \int_{-1}^{0}{\frac{3}{x-1} - \frac{1}{x+2}} dx[/math]. C'est fou comme la nature est bien faite, on sait intégrer cette expression.
[math][3ln|x-1| - ln|x+2|]_{-1}^{0}[/math] (pensez bien à mettre les valeurs absolues car x-1 est négatif sur [-1;0]) [math]= 3ln(1) - ln(2) - (3ln(2) - ln(1) ) = -4ln(2)[/math]
On a finalement pu calculer cette intégrale ;) .

Si [math]\Delta = 0[/math]

Comme tout à l'heure, prenons un exemple : [math]\int_{0}^{\frac{1}{2}} {\frac{2x+1}{x^2-2x+1} dx}[/math]. Bon, pas de mystère sur la racine, je pense. De toute manière, quand [math]\Delta = 0[/math], c'est qu'on est en présence d'une identité remarquable.[math]x^2-2x+1 = (x-1)^2[/math] d'où notre racine double 1.

Voilà comment cela se passe. Maintenant qu'on a trouvé notre racine c, on peut trouver une nouvelle écriture tel que : [math]\frac{ax+b}{x^2+px+q} = \frac{\alpha}{x-c} + \frac{\beta}{(x-c)^2}[/math].
[math]\frac{\alpha}{x-c} + \frac{\beta}{(x-c)^2} = \frac{\alpha \times (x-1)+ \beta}{(x-1)^2} = \frac{\alpha x +\beta - \alpha}{(x-1)^2}[/math]
Par identification des termes : [math]\left\{\begin{array}{l c r}\alpha = 2\\\beta-\alpha = 1 \end{array}\right. \Rightarrow \left\{\begin{array}{l c r}\alpha = 2\\\beta = 3 \end{array}\right.[/math]
D'où [math]\int_{0}^{\frac{1}{2}} {\frac{2x+1}{x^2-2x+1} dx} = \int_{0}^{\frac{1}{2}} {\frac{2}{x-1} + \frac{3}{(x-1)^2} dx}[/math]. Et comme de par hasard, on sait maintenant intégrer (à condition de connaitre ces primitives ). [math][2\times ln|x-1| - \frac{3}{x-1}]_{0}^{\frac{1}{2}} = 2ln(\frac{1}{2})+6 -(2ln(1) +3) = -2ln(2)+3[/math]

Bien, j'espère que vous êtes prêt car après ces petites mises en bouche, on attaque le plat de résistance.

Si [math]\Delta < 0[/math]
Ha, le discriminant est négatif, il n'y a donc pas de racines donc le polynôme ne peut pas se factoriser. Qu'à cela ne tienne, on va y arriver quand même. Pour cela, on va chercher à faire apparaitre la dérivé du polynôme au numérateur.

La dérivé de [math]x^2+px+q[/math] est bien entendu [math]2x+p[/math]. Cherchons à la faire apparaitre au numérateur. [math]ax+b = \frac{a}{2} \times (2x + p) + b - \frac{a\times p }{2}[/math]. On est d'accord? Développez tout et vous retrouverez bien ax +b.
Attend, pourquoi on n'a pas mis tout simplement [math]ax+b = 2x + p + (a -2)x +b-p ?[/math]
Très bonne question. En fait, le but de la manœuvre est de trouver 2x+p pour séparer sur en deux fractions. L'une donnera donc la dérivé de [math]ln(x^2+px+q)[/math] et donc dans l'autre, on doit avoir une expression plus simple à résoudre. Or si on découpe comme cela, dans la deuxième fraction, on va retrouver une expression avec des x au numérateur et cela ne va pas nous arranger. À l'inverse, dans ma transformation, on va se retrouver avec une constante multiplicative que l'on pourra donc sortir de l'intégrale.

Pour y voir plus clair, je vous propose de prendre un exemple. [math]\int_{0}^{1} {\frac{-3x+2}{x^2-x+1}dx}[/math].
Faisons apparaitre la dérivé de [math]x^2-x+1[/math] au numérateur. [math]\int_{0}^{1} {\frac{-3x+2}{x^2-x+1}dx} = \int_{0}^{1} {\frac{\frac{-3}{2} \times (2x-1)+\frac{1}{2}}{x^2-x+1}dx}[/math]
[math]= \frac{-3}{2} \times \int_{0}^{1}{\frac{(2x-1)}{x^2-x+1}dx}+\frac{1}{2}\int_{0}^{1} {\frac{1}{x^2-x+1}dx}[/math]

Et nous nous retrouvons avec un calcul bien compliqué. Pour améliorer la clarté de l'exercice et rendre les choses plus digestes, je vous propose de gérer les deux intégrales séparément.
[math]\frac{-3}{2} \times \int_{0}^{1}{\frac{(2x-1)}{x^2-x+1}dx} = \frac{-3}{2} \times [ln|x^2-x+1|]_{0}^{1} = \frac{-3}{2} \times (ln(1) - ln(1)) = 0[/math]. C'est décidément bien arrangeant. Cette situation arrive car j'ai bien choisit mon exemple, cela ne s'annule pas toujours.

Pour la deuxième, on va se servir de deux choses que je vous ai apprit plus haut, c'est-à-dire, l'arctangente et l'intégration par changement de variable. En effet, je rappelle que [math](arctan(x))' = \frac{1}{x^2+1}[/math]. Qui avait oublié?
Et ici, on a [math]\frac{1}{2}\int_{0}^{1} {\frac{1}{x^2-x+1}dx}[/math]. [math]x^2-x+1[/math] est presque une identité remarquable (comme tout les polynômes du second degrés). En effet, c'est presque [math](x-\frac{1}{2})^2[/math] car [math](x-\frac{1}{2})^2 = x^2 -x +\frac{1}{4}[/math]. Pour retomber sur notre expression, il suffit d'ajouter [math]\frac{3}{4}[/math]. Ainsi [math]\frac{1}{2}\int_{0}^{1} {\frac{1}{x^2-x+1}dx} = \frac{1}{2}\int_{0}^{1} {\frac{1}{(x-\frac{1}{2})^2 + \frac{3}{4}}dx}[/math] .
Maintenant on a [math]+ \frac{3}{4}[/math] alors qu'on souhaite un +1 :( . Pas de problème, on a qu'à factoriser par [math]\frac{3}{4}[/math]. On obtient donc [math]\frac{1}{2}\int_{0}^{1} {\frac{1}{\frac{3}{4}\times (\frac{4}{3}(x-\frac{1}{2})^2 + 1)}dx}[/math].
Mince, maintenant, on a plus une expression au dénominateur de la forme [math]x^2 +1[/math] :( . Mettons alors le [math]\frac{4}{3}[/math] dans le carré, on en profite pour sortir [math]\frac{3}{4}[/math] de l'intégrale puisque c'est une constante multiplicative. Mais attention, n'oubliez pas qu'il faut sortir non pas [math]\frac{3}{4}[/math] mais son inverse [math]\frac{4}{3}[/math].
On finit par avoir : [math]\frac{1}{2}\times \frac{4}{3}\int_{0}^{1} {\frac{1}{(\frac{2}{\sqrt{3}}(x-\frac{1}{2}))^2 + 1)}dx} = \frac{2}{3}\int_{0}^{1} {\frac{1}{(\frac{2}{\sqrt{3}}(x-\frac{1}{2}))^2 + 1)}dx}[/math]

Il nous reste plus qu'à poser [math]t = \frac{2}{\sqrt{3}}(x-\frac{1}{2})[/math]. Et oui, on va faire une intégration par changement de variable. On en déduit que [math]\frac{dt}{dx} = (\frac{2}{\sqrt{3}}(x-\frac{1}{2}))' \Rightarrow \frac{dt}{dx} = \frac{2}{\sqrt{3}} \Rightarrow dx = \frac{\sqrt{3}}{2}dt[/math].
Quant aux nouvelles bornes :[math]0\leq x \leq 1 \Rightarrow \frac{-1}{2}\leq x-\frac{1}{2} \leq \frac{1}{2}\Rightarrow \frac{-1}{\sqrt{3}}\leq t \leq \frac{1}{\sqrt{3}}[/math]

On a donc une nouvelle écriture pour notre intégrale qui est : [math]\frac{2}{3}\int_{\frac{-1}{\sqrt{3}}}^{\frac{1}{\sqrt{3}}} {\frac{1}{t^2 + 1}\times \frac{\sqrt{3}}{2}dt} = \frac{\sqrt{3}}{3}\int_{\frac{-1}{\sqrt{3}}}^{\frac{1}{\sqrt{3}}} {\frac{1}{t^2 + 1}dt}[/math]

Ha ! C'est quoi cette intégrale. Et si je vous disais qu'on peut la simplifier. Arc tangente est la fonction réciproque de tangente. Une fonction réciproque est une fonction dont la courbe représentative de la fonction réciproque est symétrique à la fonction dont elle est la réciproque par rapport à la droite d'équation [math]y = x[/math]. Autrement dit, une fonction impaire a comme réciproque une fonction paire. Et il se trouve que tangente est impaire donc arctangente est donc paire. De plus [math][\frac{-1}{\sqrt{3}};\frac{1}{\sqrt{3}}][/math] est un intervalle centré sur 0. Appliquons donc nos formules sur la parité.

[math]\frac{\sqrt{3}}{3}\int_{\frac{-1}{\sqrt{3}}}^{\frac{1}{\sqrt{3}}} {\frac{1}{t^2 + 1}dt} = 2 \times \frac{\sqrt{3}}{3}\int_{0}^{\frac{1}{\sqrt{3}}} {\frac{1}{t^2 + 1}dt} = \frac{2\sqrt{3}}{3}[Arctan(t)]_{0}^{\frac{1}{\sqrt{3}}} = \frac{2\sqrt{3}}{3} ( Arctan(\frac{1}{\sqrt{3}}) - Arctan(0))[/math].

On sait que Arctan(0) = 0 mais qu'en est-il de [math]Arctan(\frac{1}{\sqrt{3}})[/math]? Il faut que [math]tan(y) = \frac{1}{\sqrt{3}} \Rightarrow \frac{sin(y)}{cos(y)}= \frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}}[/math]. Si vous connaissez votre cercle trigonométrique, vous avez comprit que l'angle à trouver était [math]\frac{\pi}{6}[/math].
Donc [math]\frac{2\sqrt{3}}{3} ( Arctan(\frac{1}{\sqrt{3}}) - Arctan(0)) = \frac{2\sqrt{3}}{3} \times \frac{\pi}{6} =\frac{\pi\sqrt{3}}{9}[/math]

Ca y est, enfin, on a finit. On a prouvé que [math]\int_{0}^{1} {\frac{-3x+2}{x^2-x+1}dx} = \frac{\pi\sqrt{3}}{9}[/math].
Vous avez réussit à faire cette intégrale pourtant compliquée, félicitation! Bon, ce n'est pas comme si je vous y préparais depuis le début. Mais avouez que vous ne pensiez pas tomber sur de telle cas durant ce cours.