Le format papier et racine de 2

Vous le savez surement, on utilise traditionnellement des feuilles de papier au format A4, c'est-à-dire, 21 x 29,7 cm. Vous ne vous êtes jamais demandé pourquoi on a choisi cette taille? Après tout, à la découpe, prendre 29,7 cm ne doit pas être des plus aisés. Pourquoi ces 0,7 centimètres? Et puis, pourquoi le format le plus utilisé est A4? Pourquoi ne l'a-t-on pas appelé A0 et on partirait de lui comme format de référence.

Il faut savoir que cela a été normalisé via l'ISO 216 et est donc internationalement utilisé. Ce n'est donc pas irréfléchi ni un choix anodin. En effet, c'est un choix très pratique et non, ce n'est en réalité pas difficile d'avoir à la découpe. Ils ont fait en sorte que lorsqu'on coupe une feuille au format X(n), cela nous donnerait deux feuilles au format X(n+1). Je mets deux A4 à côté et on obtient une A3. Et si je plie une A4 dans la longueur alors j'obtiendrai une A5. La dessus, je pense ne rien vous apprendre.

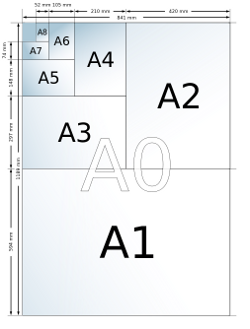
Mais cela ne suffit pas. Car j'ai envie de dire, je coupe par la diagonale et j'obtiens deux triangles qu'il suffit d'ajouter pour constituer le format au dessus. Il fallait garder la même forme rectangulaire et surtout garder les mêmes proportions, c'est-à-dire, que le rapport de la longueur par la largeur devait être égal au celui du format précédent. De cette façon, on aura qu'à appliquer ce rapport sur la taille du dessin ou de la police d'écriture pour le convertir au nouveau format sans que l'oeuvre soit déformée. Il se trouve que cet propriété est rendu possible grâce à racine de deux.

En effet, racine de 2 est le seul nombre à avoir cette propriété là. Pour vous en convaincre, je vous propose de regarder le schémas suivant:

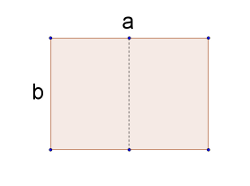
Nous avons un rectangle de longueur a et de longueur b. Et on veut que le rapport des dimensions de ce rectangle soit le même que celui du rectangle obtenu après avoir coupé la feuille en deux sur la longueur et qui a donc comme longueur b et largeur la moitié de a.

En résumé, on veut que :

Voilà pourquoi le 0,7 cm est important, pour garder la proportion à racine de 2. Après [math]\frac{297}{210} \neq \sqrt{2}[/math], c'est proche mais ce n'est pas réellement égal. Faut bien penser que cela a été fait en 1922 par la DIN (bureau de normalisation) allemande avant d'être répandu dans le monde et à l'époque, on n'avait pas des outils aussi précis que maintenant.

Alors maintenant, pourquoi A4? Car on est parti du format A0 qui est en fait, le format Aigle inventé et imposé par Napoléon Bonaparte (c'était pour imposer une échelle pour les cadastres de ville) et se voulant être une surface d'un mètre carré. L'erreur vient en réalité de là, car ils ont prit 841 × 1189 mm. Or [math]841 \times 1189 = 999\ 949 \cong 1m^{2}[/math]. Mais globalement, l'erreur est si infime qu'on ne la voit guère.