Comment couper N parts égales d'un gâteau

Mardi, c'est l'Épiphanie, cette fête où on tire les rois. Ce fameux jour où on se met tous autour d'une galette espérant tirer la fève pour être le roi de la soirée. Oui mais voilà, si le vieil oncle Bertrand prend une immense part, les autres sont désavantagés. Il en va de l'équité de tous de découper des parts égales. Or selon le nombre d'invités, ce n'est pas toujours des plus faciles. Alors comment couper N parts égales dans un gâteau, une galette et autres ronds?

En fait, il suffit d'appliquer un algorithme itératif très simple. Mais pour l'appliquer, il faut faire un petit calcul. Un rond, je ne vous apprends rien, fait 360°. Donc si on souhaite que toute le monde ait la même part, il faut que chacun ait un angle de [math]\frac{360}{N}[/math]. Prenons l'exemple suivant, on veut 9 parts. Il faudra donc que chaque part ait un angle de [math]\frac{360}{9} = 40°[/math] . Mais vient la grande question, comment prendre intuitivement 40°? Je vous propose de garder cette exemple, et de regarder le schémas ci-dessous:

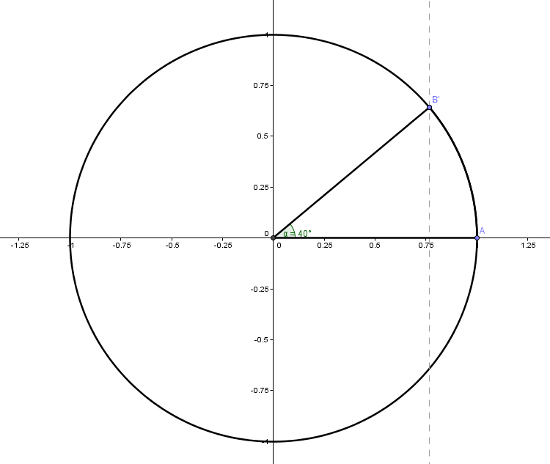
Imaginons, on a commencé par couper du centre O jusqu'au point A. On a donc un rayon de notre cercle. On va savoir où placer notre point B pour être sûr d'avoir un angle à 40°. Regardons où se croise la perpendiculaire à OA passant par B et le segment OA. La perpendiculaire a été représenté en tiret. On note qu'elle se coupe très près du 0.75. Or qu'est-ce que le 0.75? C'est les trois quarts de notre rayon et on sait très simplement calculer ça. On prend la moitié de notre rayon puis la moitié du segment supérieur. Donc, on fait ça, on remonte légèrement plus et après, on prend la perpendiculaire et on regarde sur quel bord de la tarte/galette/gâteau j’atterris. Je n'ai plus qu'à découper du centre à ce bord, ici découper OB.

Ok mais après? Bah A, je l'ai pris totalement arbitrairement. J'ai pris un rayon quelconque et je me suis débrouillé pour en avoir un autre. Imaginons que je prend comme rayon OB, serais-je capable d'appliquer la même méthode pour trouver une autre part? Oui en effet. Il me suffit de reprendre un petit peu plus de 75% de OB et partir perpendiculairement jusqu'à bord de mon cercle et là, j'ai une nouvelle part encore. Et je continue ainsi jusqu'à la fin de mon gâteau. Et comme on est parti de 360°, normalement, il ne devrait pas y avoir de résidu en plus. Exemple avec cette galette qui nous vient de "Le sot l'y laisse" :

Alors vous allez me dire "ok mais si je ne souhaite pas neuf parts mais 6?". Eh bien la logique est exactement la même. La seule donnée qui vous manque est le pourcentage du rayon à prendre. Comme on veut 6 parts, on veut des parts avec des angles de 60°. Plutôt que de regarder à la louche un schémas, pour obtenir ce fameux pourcentage, on doit juste fait en réalité [math]cos(60°) \times 100[/math]. En général, [math]cos(\frac{360}{N}) \times 100[/math] avec N, le nombre de parts souhaité. Il se trouve que pour 6 parts, [math]cos(60°) = 0.5[/math] donc on doit juste prendre la moitié de notre rayon. J'imagine que vous n'avez pas toujours une calculette dans la main quand vous coupez un gâteau donc voici ce qu'il faut se souvenir:

PS: Si vous êtes 13, pensez plutôt à prendre une autre galette car on mange peu avec un treizième du gâteau.