Est-ce qu'un processus infini peut se terminer? Voilà une question forte intéressante. "Stupide" diront certains sans comprendre toute la subtilité scientifique derrière. "C'est trivial" diront d'autres, "par définition, ça n'a pas de fin". La question est en réalité plus subtile que ça car on ne parle pas de fin, on parle de terminer, d'un après, peut-il y avoir un "après" lors d'un processus infini?

Je m'explique. Connaissez-vous le paradoxe de la dichotomie? Il fait parti des fameux paradoxes de Zénon d'Élée, philosophe grec présocratique du Ve siècle avant J.C. Concrètement, il se présente comme sui: Zénon se tient à huit mètres d'un arbre et veut y lancer une pierre. Pour atteindre l'arbre, la pierre va d'abord devoir parcourir la moitié de la distance, soit 4m, puis la moitié des 4m restant, donc 2m, puis ainsi de suite. À chaque itération, il va devoir parcourir la moitié de la distance restante et ce, indéfiniment. Du coup, jamais la pierre ne touchera l'arbre car c'est un processus infini. C'est absurde, je pense que vous pourrez tous attester que la pierre touchera l'arbre (si tant est que Zénon vise bien). Pourtant, si je suis mon raisonnement, jamais il n'est censé le toucher car il restera toujours à la pierre à parcourir l'autre moitié de la distance restante. Que dire alors?

"Simple! Tu ne m'auras pas, Yann. On parle ici du monde réel! Or le monde réel est bornée par la physique. Or la physique nous dit qu'il y a, à un certain niveau, un élément insécable, qu'on ne pourra plus diviser en deux. Pendant longtemps, ce fut l'atome en tant que tel puis avec nos avancées modernes, c'est le quantas qu'on ne peut réduire. Basée sur la constante de Planck, utilisée pour décrire la taille des quantas, la longueur de Planck est une distance qu'on ne peut, à ce jour, physiquement pas réduire. Celle-ci est de [math]l_p = 1.616252 \times 10^{-35}m[/math]. On ne peut alors pas dans le monde réel diviser par deux la distance entre la pierre et de l'arbre indéfiniment! Donc ça ne marche pas car ce n'est pas un processus infini."

Bah Billie, tu as pris des cours depuis notre dernière rencontre? Bah tu sais quoi? Ce que tu dis est vrai. On ne peut pas physiquement diviser continuellement par deux, on est borné par la constante de Planck et ce qui en découle. En outre, même si on remettait en cause cette constante et trouverait un élément encore plus petit, on ne ferait que réduire cette valeur mais elle ne sera jamais infini. Cependant, on est d'accord que quand le monde abstrait des maths, on peut. Représentons mathématiquement le cheminement de la pierre. On est d'accord qu'à chaque étape, je vais devoir ajouter à la distance précédente un demi de elle-même, ce qu'en terme de suite, on dirait [math]u_{n+1} = \frac{1}{2}u_n[/math]. Et on va faire la somme des éléments de cette suite. Appelons cette somme S et la distance à traverser d. On a donc :
[math]S = \frac{1}{2}d + \frac{1}{4}d + \frac{1}{8}d + \frac{1}{16}d + ...[/math]
Multiplions S par 1/2 :
[math]\frac{1}{2}S = \frac{1}{4}d + \frac{1}{8}d + \frac{1}{16}d + ...[/math]
Et si je soustrais les deux équations, que se passerait-il? Tous les éléments qui continuent à l'infini s'annuleront sauf le premier. On obtiendra :
[math]\frac{1}{2}S = \frac{1}{2}d \Rightarrow S = d[/math]
La distance sera donc atteinte...même dans le monde des mathématiques sans constante de Planck. Car oui, Billie, une somme infinie peut arriver à un résultat fixe et déterminé. L'un des exemples les plus parlant est le suivant:
[math]S = 0.9999...\\
10S = 9.9999...\\
10S = 9 + 0.9999...\\
10S = 9 + S\\
9S = 9\\
S = 1\\
1 = 0.9999...[/math]
Ceci n'est valable que pour l'infini. Il ne peut pas y avoir de dernier 9 sans quoi ça ne serait plus égal mais à l'infini, c'est réellement égal. 1 = 0.9999.... Tout comme [math]d = \frac{1}{2}d + \frac{1}{4}d + \frac{1}{8}d + \frac{1}{16}d + ...[/math]

"Une addition infini qui se traduit par un nombre défini... Je ne sais quoi dire. Tu es sûr qu'il n'y a pas erreur? Que ce n'est pas un raisonnement par l'absurde par exemple". Ok, je vais prendre un autre exemple. On va parler des supertask et de la lampe de Thomson. J'allume une lampe puis j'attends une minute. J'éteins alors la lampe et j'attends moitié moins de temps donc 30 secondes. Je rallume ma lampe et j'attends 15 secondes et je continue le processus d'allumer et d'éteindre la lampe indéfiniment. Comme je divise le temps d'exécution par deux à chaque fois, on est d'accord que comme pour le paradoxe de Zénon, on a ici un processus infini. Or, pour ce processus infini, je réduis le temps de chaque étape de moitié ce qui fait que ce processus infini va durer un instant fini. Au passage, c'est ça qu'on appelle une supertask. Car in fine, qu'y a-t-il à 2 minutes? La lampe est-elle allumée ou éteinte? Car l'infinité des actions s'est déroulée dans ces deux minutes si vous regardez bien. La somme ne va pas nous aider cette fois car elle diverge entre deux états (allumé 1 et éteint -1) qui n'est pas sans rappeler cet article où l'on trouve que la réponse est 1/2 donc que ça peut être soit l'un, soit l'autre. On ne peut le déterminer.

Paul Benacerraf vient alors à notre aide dans son écrit "Tasks, super-tasks, and the modern eleatics". Il souligne que nous sommes incapable de déterminer l'état de la lampe car nos informations ne sont pas complètes. On a mélangé le monde réel (la lampe) et le monde mathématique. Comment fait-on pour que la lampe alterne d'état? Si par exemple, c'est une boule électrique rebondissant sur une plaque conductrice dont la hauteur diminue à chaque fois de moitié comme sur le dessin ci-dessous, alors là, on est capable de déterminer :


Car on connaît ici la situation finale, la boule cessera de rebondir à la fin de notre supertask et cela nous permet de déduire la situation finale de la lampe en fonction du circuit électrique utilisé. Le fait de mathématiquement pas pouvoir déterminer la situation finale est justement du à cette abstraction du monde mathématique, voilà tout. Il n'en reste pas moins qu'il est totalement possible pour un processus infini de se terminer.

On continue notre série sur les travers de notre système électoral. Après le système de vote, il est temps de nous attaquer au découpage électoral. Cette problématique se pose lorsqu'on doit élire non pas un conseil dans sa globalité mais qu'on vote que pour une constituante, une partie de celui-ci.

De quoi je parle? Vous voyez les élections municipales en dehors des 3 plus grandes villes de France qui ont un traitement spécial (Paris, Lyon Marseille)? Vous votez ici par un vote majoritaire pour l'entièreté du conseil. Le vainqueur remporte plus de la moitié des sièges et le reste est partagé proportionnellement. Bien qu'on peut critiquer le scrutin majoritaire, on note qu'ici, nous maitrisons totalement la composition du conseil, de façon à représenter la volonté des habitants de la ville. Normalement, la liste qui a remporté les suffrages représente bel et bien la majorité de la population ayant votée (le vote blanc n'étant pas décompté). Rien d'anormal. Cela vous semble même logique. Cela serait étrange que le parti vainqueur ne soit pas celui qui soit le plus représenté.

Pourtant, c'est ce qui peut arriver lorsqu'on vote par circonscription, par zone si vous voulez. C'est le cas par exemple pour les élections législatives où différentes circonscriptions élisent leurs députés. C'est aussi le cas pour les sénatoriales où on vote une liste par département. Il y a enfin les cantonales qu'on a appelé départementales où chaque canton vote pour un représentant au conseil général qui s'appelle maintenant conseil départemental (et mais c'est que ça bouge quand même). Bon, et du coup, où est le problème, me direz-vous? Chacun des territoires choisit un représentant pour siéger à un conseil d'un niveau plus grand. Qu'est-ce qu'il y a de mal? Les limites de ces territoires ne sont pas marquées dans le marbre. En fonction de la démographie, de l'évolution du territoire et de sa population ou encore par simple volonté politique, les limites bougent et se redéfinissent. Et on n'en parle jamais mais ce n'est pas si rare que ça. Les lignes pour les législatives ont bougé en 2009, les cantons ont été réduits par deux en 2013 (ce qui a valu qu'on repousse les élections départementales et régionales en 2015). Or celui qui redessine les lignes maitrisent totalement le scrutin.

Je m'explique. Imaginez un pays super simple avec 100 villes que je vais représenter ici par un carré de 10x10. Globalement, par le jeu des statistiques, des sondages, des résultats précédent, on sait déjà globalement pour qui la ville va voter. Toujours pour simplifier, on ne va prendre que 2 partis, les rouges et les bleus. Disons qu'il y a 40 villes pour les bleus et 60 pour les rouges. On vient de nous donner comme mission de découper le territoire en 10 circonscriptions. Dans l'idéal, je peux faire en sorte que la proportion (60% de bleu et 40% de rouge) soit respectée au sein du conseil. Il me suffit de découper le territoire comme suit:



Mais voilà, moi je suis pro-rouge ou bien les rouges m'ont tout simplement acheté. En jouant avec les lignes, je suis capable de faire en sorte que la totalité du conseil soit rouge. Si, si. C'est juste un petit jeu géométrique.



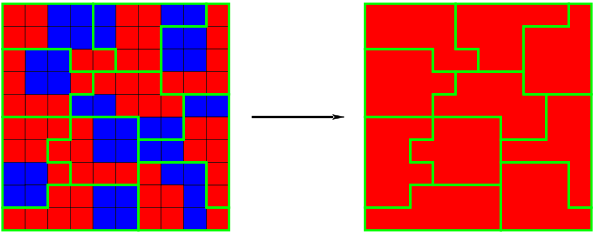
Sachez que les bleus peuvent également m'acheter et bien que je ne peux leur donner la totalité (car ils n'ont pas la majorité des villes), je peux quand même leur donner la majorité au conseil auquel ils candidatent. Il suffit que je coupe comme sui et ils auront 60% :



C'est ça le gerrymandering. C'est le fait de découper le territoire dans le but de favoriser un parti. C'est un mot qui nous vient des États Unis, en 1981 pour dénoncer les dérives du découpage électoral. Le Gerrymandering est un vrai problème et n'affecte pas juste mon petit schéma ci-dessus. On a notamment eu le cas récemment avec l'élection présidentielle américaine où malgré que la population ait voté majoritairement pour Hillary, par le jeu des swing-states et donc du découpage électoral, c'est Trump qui a reçu le plus de grands électeurs et sera normalement sacré président. Ce fut également le cas pour les élections présidentielles américaines de 1876, 1888 et 2000, où les démocrates, bien que majoritaires dans l'électorat, furent battus à cause du découpage des États.

Le problème du vote par zone est l'effet de seuil. En réalité, pour gagner, seul suffit 50.01%. Le reste des votes n'est que surplus et est donc perdu alors qu'ils auraient pu aider une autre zone pour faire basculer le parti. Car que vous gagnez avec 50.01% ou 100%, cela importe peu. Vous avez remporté votre zone mais ça ne change rien au niveau de la composition du conseil. De même, lorsqu'on perd, l'ensemble de nos votes pour le perdant sont eux-mêmes perdus. C'est d'autant plus rageant si le vainqueur n'a que 51%. Youhou, 49% de la zone n'est pas représenté. Alors que ces voix auraient elles aussi permis peut-être de récupérer une autre zone (et donc un siège).

Mais critiquez, c'est mignon. Proposez des solutions, c'est meilleur. Quelles sont les alternatives? La plus naturelle est évidemment de donner le découpage des lignes électorales à un organisme indépendant. Mais peut-on réellement être indépendant? Je préfère une autre solution, plus pragmatique. Vous avez peur que cet organisme se fasse acheter par un des partis pour le favoriser? Payez le pour qu'ils fassent en sorte de faire un découpage correspondant au mieux aux proportions nationales. Si je reprends mon exemple de 100 villes. Je vais demander à l'organisme de me faire un découpage pour que la composition du conseil colle au mieux du 60% rouge et 40% bleu et je ne paierai que si c'est le cas. En quelque sorte, on fait du gerrymandering mais là, ce n'est pas les partis mais l'État qui paie pour que le conseil soit représentatif de sa population. C'est quand même mieux et c'est cool car ça ne serait plus aux politiques de le faire. Seulement ça coute des sous...mais ça garantie une bonne représentativité.

On peut aussi supprimer les zones et faire un vote à la proportionnelle. On voterait alors pour une liste comme pour les municipales et ça serait une élection nationale. Cependant, dans ces cas là, on ne sera pas sûr que notre territoire soit représenté. Cela peut moralement poser problème et vous en êtes seul juge. Mais bon, si on nous sort une liste avec essentiellement des Parigos, avec tout le respect que j'ai pour eux, avouons que l'assemblée ne sera guère représentative de la diversité du territoire. On impose une personne de chaque territoire dans la liste? S'il gagne 60%, comment décide-t-on de ceux qui vont siéger? De quel droit, via des arrangements internes, va-t-on écarter tel territoire plutôt qu'un autre?

On peut aussi découper le territoire non pas par un choix humain mais par les mathématiques. Il existe de nombreux algorithmes pour découper une zone de N éléments en M circonscriptions. Je pense, par exemple, au Shortest Split Line Method que j'aborderai surement un jour dans ma rubrique mathématique. Pour le moment, je ne vais pas rentrer dans les détails mais je peux vous assurer qu'il existe des méthodes "neutres" pour découper une zone en x sous-zones / circonscriptions. Alors bien sûr, cela peut totalement aboutir à une situation, un découpage qui va favoriser un parti plutôt qu'un autre, mais ça sera purement fortuit, ça ne sera pas voulu par l'Homme, il n'y aura pas eu de malversation de l'Homme, c'est une machine qui a découpé, tout simplement.

La fausse bonne idée serait de proposer de découper les zones et de les soumettre à l'approbation des partis. Alors déjà, je ne vous raconte pas le bordel pour mettre tout le monde d'accord. Et surtout, il faut bien voir que les partis n'ont pas les mêmes intérêts que les électeurs. Les électeurs veulent des élections serrées où le candidat doit se battre et donc convaincre pour arriver premier. Cela permet ainsi de donner du poids au peuple. À l'inverse, les candidats, eux, veulent surtout un vivier facile pour avoir leur place assurée et donc conserver leurs privilèges. Et c'est ainsi qu'on se retrouve avec toujours les mêmes, indéboulonnables, tout simplement car ils se seront répartis en terrain conquis. Pour illustrer, imaginez-vous juste 4 zones, 2 bleus et 2 rouges, que vous devez couper en deux. Pour les électeurs, le meilleur serait de faire un découpage en deux zones "1 bleu et 1 rouge". Comme ça, chacun va devoir convaincre, se battre, céder sur des points pour faire plaisir aux électeurs.... Les partis, eux, veulent s'assurer d'être présent, d'avoir le siège. Ils ne veulent pas d'une guerre incertaine. Ainsi ils vont préférer une zone "2 bleus" et une autre "2 rouges" où chacun gagne un siège assurément. Mais derrière, il n'y a aucun challenge, aucun risque et donc si on a aucun risque, pourquoi le candidat se plierait aux réclamations de quelques uns?

Le Gerrymandering est un sérieux problème qui peut totalement défaire le résultat d'une élection. Ainsi, il nous appartient d'être vigilant lorsque les lignes bougent. Mais sincèrement, aujourd'hui, qui s'en soucie? Personne. Le saviez-vous que les circonscriptions avaient bouger en 2009? Saviez-vous que les cantons aussi en 2013? Cela fait beaucoup moins de bruit que la réduction par deux de nos régions et pourtant d'un point de vue électoral, c'est beaucoup beaucoup plus important. Des solutions, il y en a, en gardant les zones, en les enlevant, en virant le politique du processus, en payant pour assurer une équité. Maintenant, encore faut-il des voix pour réclamer le changement. Un certain président avait annoncé que le changement, c'était maintenant mais sur le fond, in fine, pas grand chose a changé et personne ne s'ose à aborder le sujet. On préfère se cristalliser sur "faut-il faire voter les étrangers" plutôt que sur "comment rendre notre système électoral plus juste"...

Notre système électoral pour les présidentielles et les législatives, soit les deux élections les plus importantes pour le fonctionnement de l’État, est assez simple et dérive du système « First Past The Post » à la subtilité qu’il s’exécute en deux tours. Il fonctionne comme sui, chaque personne n’a qu’une seule et unique voix qu’elle ne peut donc donner qu’à un seul candidat et celui qui a le plus de voix remporte l’élection. Il y a toutefois deux tours où les conditions varient pour être sélectionné au second tour. Pour les présidentielles, c’est les deux meilleurs, point. Et les législatives, il faut atteindre un certain pourcentage. Si on a déjà la majorité absolue au premier tour (plus de 50% des voix), alors on est directement élu sans second tour. Ce système s’appelle le scrutin uninominal majoritaire à deux tours. Il est simple, logique et juste…n’est-ce pas ?

Hé bien en réalité, pas du tout. Personnellement, je suis contre ce système de vote et je vais vous expliquer pourquoi. Pour cela, on va imaginer une situation comme ci-dessous au premier tour (ceci est de la fiction, je ne vise aucun pays ou parti, soyons clair) :

- L’extrême gauche : 9%
- Divers gauche : 18%
- Gauche : 19%
- Centre : 13%
- Droite : 20%
- Divers droite : 15%
- Extrême droite : 6%

En second tour, les vainqueurs seront soit la gauche, soit la droite. Cela pose déjà un problème car bien que les gens se sont rabattus sur ces candidats au second tour, in fine, cette personne est élue alors que 80% des personnes n’ont pas voté pour elle. La minorité domine. Ce fut le cas au Venezuela par exemple où, en 1993, Rafael Caldera fut élu président avec 30,5% des voix exprimés. Mais ça, j’ai envie de dire, ce n’est pas le pire.

Là où c’est plus embêtant, c’est que cela amène irrémédiablement à un système à deux partis comme c’est le cas actuellement en France avec le parti socialiste et les républicains. Et c’est normal. Car au fil des élections, c’est eux qui l’emportent avec ce système. Donc petit à petit, les électeurs de partis minoritaires s’effritent pour voter « utile », aussi appelé le « spoiler effect ». Ainsi les extrêmes n’aiment vraiment pas l’autre côté (droite ou gauche). Ainsi pour éviter de les faire élire, ils vont plutôt voter pour celui qui a le plus de chance d’être élu. Ainsi, on vote pour le moins pire et non plus pour ce qu’on souhaite afin d’éviter que celui qu’on déteste l’emporte. Du fait qu’on ait qu’une voix, les candidats divers ne font qu’amoindrir en réalité la branche du courant principal. Le stock de voix qui est proche de la droite, par exemple, aurait pu lui permettre de passer devant la gauche. Heureusement, le second tour permet ce report mais ça ne change rien au fait que les petit-partis sont défavorisés par le « vote utile ». Pour un parti divers droite, pour faire gagner la droite, il ne devrait pas se présenter pour éviter de diviser les voix…c’est stupide. Les courants de droite et de gauche consolidés par cela font que c’est les deux grands vainqueurs, le centre perd naturellement et doit donc se répartir au second tour entre les deux. Vous pouvez dire « fuck le système, votez le 3e parti ». In fine, vous ne ferez que favoriser le parti adverse. Ce n’est pas de votre faute, c’est le système qui est comme ça. Donnez-lui suffisamment de temps et il deviendra un système bipartisme.

Enfin, ce n’est pas un système respectant le critère Condorcet. C’est une incohérence soulevée au XVIIIe siècle par un mathématicien français, Nicolas de Condorcet. On a un gagnant Condorcet lorsqu’on choisit une personne qui deux à deux vainc un maximum de candidats. Je m’explique en reprenant l’exemple de Wikipédia :

Sur 21 électeurs, voici leurs choix (par ordre de préférence)
7 électeurs choisissent : A puis C puis B ;
8 électeurs choisissent : B puis C puis A ;
6 électeurs choisissent : C puis A puis B.

Dans ce système, le candidat C est éliminé dès le premier tour alors qu'il aurait gagné son duel contre A (A : 7 et C : 14 si B n’existait pas) et son duel contre B (B : 8 et C : 13 si A n’existait pas).

« Ok, Yann, t’es mignon et je vois que tu te complais dans ton rôle d’opposition. Tu critiques bien et c’est vrai que ce n’est pas l’idéal. Mais est-ce que tu as mieux ? Car pour citer Churchill : « La démocratie est le pire des régimes - à l'exception de tous les autres déjà essayés dans le passé ». Là, c’est un peu pareil. Tu souligne les erreurs mais y a-t-il mieux ? »

Tout d’abord, merci de dire que je suis mignon. Hé sinon, oui, j’ai des alternatives à proposer. Je tiens juste à préciser que je ne vais parler dans cet article que du système de décomptes des votes. Il y a bien des choses à changer comme la reconnaissance du vote blanc ou le gerrymandering (découpage électoral). Mais ça fera l’objet d’autres articles dédiés tant c’est un vaste sujet.

Globalement, faut arrêter le fait d’avoir une seule voix. C’est ce qui cause le vote utile. On ne doit pas gaspiller notre voix et ce qui tue les petits partis, car on préfère la donner à ceux qui ont des chances de gagner. Comment faire alors ? Plutôt que de voter pour un candidat, il faut simplement voter pour tous les candidats. Une des solutions que je propose est tout simplement d’établir une liste de préférence. Ainsi, une personne d’extrême droite mettrait ce parti en première position, puis la droite en 2e puis divers droites en 3e puis le centre en 4e, la divers gauche en 5e, la gauche en 6e et enfin l’extrême gauche en 7e. Ici, on ne vote plus pour un seul parti. J’ordonne simplement les partis en fonction de mes affinités avec eux. Évidemment pour l’exemple, j’ai pris des partis mais cela marche aussi avec des candidats. Du coup, au dépouillement, on prend les premiers choix de chacun. Si personne n’a 50% alors on va éliminer celui qui a le moins de voix. On prend alors le tas des personnes ayant voté pour ce parti et on les répartit en fonction de leur second choix. Et on continue ainsi jusqu’à ce qu’un parti arrive à 50%. En agissant de cette manière, lorsqu’on vote pour un parti, on ne défavorise plus le parti de la tendance la plus proche qui aurait plus de chances de gagner. On ne divise plus les votes car une fois notre candidat éliminé, notre vote se rabat sur celui d’après dans notre liste de préférence. On ne gaspille donc plus notre voix lorsqu’on vote pour un mini-parti dont on est plus proche. Ainsi ça permettra d’avoir beaucoup plus de places pour les partis autre que les deux grands, ça leur permettrait réellement de voir combien ils pèsent (en regardant le premier tour du dépouillement) et donc de peser plus de poids face aux gros dans la défense de leurs idées (et donc des vôtres). Enfin, ça arrêtera le vote utile causé par le bipartisme. Mais est-ce la panacée ? Non, car bien que ce système soit plus juste, il est aussi plus chiant. En effet, le dépouillement doit, du coup, être itératif. On fait un premier dépouillement, on prend celui qui a le moins de voix, on l’élimine et on reporte les votes et on continue jusqu’à ce qu’on ait un candidat à 50%. Cela peut être long et rébarbatif sur des milliers de bulletins et sachant qu’on a déjà du mal à trouver des dépouilleurs… En outre, ce système ne respecte pas non plus le critère Condorcet car votre liste de préférences n’intervient que lors de l’élimination de votre candidat pour voir le report de votre voix. Mais en dehors de ça, votre ordonnancement n’a que peu d’importance dans le sens où ça ne pénalisera pas celui que vous mettez en dernier par exemple.

Alors je propose un autre système encore. On vote encore pour tous les candidats mais non plus juste « oui » / « non » mais avec une échelle de valeur du type -2 ; -1 ; 0 ; 1 ; 2. Le but va être d’entourer l’affinité qu’on a avec le candidat. 2, c’est « J’aime vraiment beaucoup le candidat », 1 pour « ça va, je l’aime bien », 0 pour « pas d’avis particulier, -1 pour « je ne l’aime pas » et -2 pour un « je ne l’aime pas du tout. Ainsi pour dépouiller, on prend juste tous les bulletins et on additionne la valeur courante du candidat (initialement 0) avec les valeurs du bulletin. Ainsi rien ne nous empêche de soutenir des petits candidats car ce n’est pas exclusif. On peut mettre 2 à la droite et à la divers droite par exemple. Cela permettrait de voir qu’elles sont les candidats vraiment appréciés des gens et non plus les votes stratégiques / utiles. Le dépouillement se fait en un tour et assez simplement car se compose juste d’addition. Et puis, voilà enfin un système respectant le critère Condorcet. En effet, comme vous jugez l’ensemble des candidats avec une note, sa position relative à tous les autres est prise en compte. On regarde au global s’il est apprécié ou pas. On ne se contente plus de ne regarder que les premiers. On va donc prendre le candidat qui a le plus de « sympathie » mais aussi le moins clivant. En effet, si on met en dernier un parti, cela va avoir un impact sur ce dernier car ça va lui faire perdre deux points. Donc ici, l’entièreté de vos préférences est prise en compte pour sortir le meilleur candidat ou du moins, celui qui fait le meilleur compromis.

J’aime beaucoup ce dernier système de vote et je me demande pourquoi on ne l’a pas encore imposé. Il faut dire que les habitudes ont la vie dure mais c’est pourtant du bon sens. L’uninominal engendre le vote utile qui est une calamité pour la démocratie mais qui est un impératif dans le système actuel. Moi je suis pour la pluralité des partis, pour que voter pour un parti plus modeste n’impacte pas ma tendance politique globale. Alors évidemment, ce n’est pas tout, il y a de grands chantiers à mener sur la reconnaissance du vote blanc et le gerrymandering mais ça sera pour une autre fois.

Aujourd'hui, en ce post, je vous propose une aventure qui vous emmènera jusqu'au tréfonds des enfers grecs. Pourquoi cet univers? C'est un peu circonstanciel vu que je lis la divine comédie de Dante et car c'est un super univers qui va permettre de romancer les énigmes et de vous offrir ainsi un voyage, une expérience, une histoire, en plus de la simple résolution des énigmes que je vais vous proposer. Ces énigmes ne seront pas toutes de moi, il y en aura même beaucoup qui ne seront pas de moi. Mais je tâcherai d'en concocter quelques unes à l'instar de mes méta-énigmes. Bien, voilà qui est tout dit. Il ne me reste plus qu'à vous souhaiter une belle épopée.



"Réveillez-vous!" Cette voix résonne dans votre tête. Alors que vous reprenez doucement vos esprits, votre oreille interne vous alerte que vous tanguez. Alors que vous ouvrez les yeux, vous vous trouvez sur une petite barque, un vieillard cagoulé ramant lentement. Tout autour se trouvait une étendue d'eau qui se terminait par un voile de brume vous empêchant de voir l'horizon.
"Je n'ai pas pour habitude de prendre des personnes gratuitement. Tous doivent payer d'au moins une obole pour traverser l'Achéron. Cependant, vous êtes spécial et méritez ainsi un traitement de faveur de la part d'Hadès en personne. Je me nomme Caron. Je serai votre nocher. Je vais vous guider vers des terres où milles épreuves vous attendent. Vous devrez y prouver votre valeur pour que Minos, Eaque et Rhadamanthe vous jugent apte à rejoindre la place qui vous revient."
Des milliers de questions vous passent par la tête mais vous n'arrivez étrangement pas à les poser. Vous vous contentez d'écouter Caron alors que vous vous redressez et vous assoyez convenablement sur la barque. Vous savez qui il est. C'est un passeur d'âmes. Cette entité psychopompe vous emmène aux enfers...vous êtes mort. "C'est vrai, continua Charon, vous êtes mort. Vous vous doutiez que cela viendrait un jour. Aux enfers, il n'y a pas de faux semblant, pas d'hypocrisie ou de manipulation, les gens sont entiers et correspondent à leur penchant. Ainsi, vous n'y trouverez que des honnêtes qui diront toujours la vérité et des menteurs qui ne feront que de mentir. Ce manichéisme a certaines vertus dont vous devrez tirer profit durant votre épopée.
- Ha ha ha, ricana une voix venue du ciel. Si tel est le cas, alors pourquoi devrait-il te croire Charon? Qui nous dit que tu n'es pas un menteur?
- Qui ose interrompre notre voyage? s'écrit le vieil homme, visiblement en colère.
- Et vous? demandez-vous, criant au ciel. De quel côté êtes-vous, vous qui vous en prenez à mon nocher? Êtes-vous un honnête?" Nul ne répondit. Caron brisa alors le silence. "S'il devait répondre, il vous dira oui".
Par cette simple affirmation, vous savez désormais si vous pouvez vous fier à Caron et si ce dernier est honnête ou menteur.

Quelques temps passèrent dans le silence alors que vous avanciez lentement au rythme des brassées de Caron. "On en a encore pour longtemps?
- Un certain temps. Vous savez, ce n'est pas comme si cela importait vraiment. Ceux qui rentrent en ces lieux y sont généralement pour l'éternité.
- Et donc vous, vous faîtes tout le temps cette traversée. Cela doit être rébarbatif. Vous n'avez jamais eu envie de voir ailleurs?
- Ma tâche est nécessaire. Fut un temps où je n'étais point là et les pauvres âmes damnées semaient tellement le désordre. Je me souviens d'un jour où trois maitres et trois esclaves sont arrivés sur la rive. Déjà, je peux te dire qu'ils n'avaient pas inventés la lance. Parmi eux, qu'un seul esclave et un seul maitre savait se servir d'une barque. Ce n'est pourtant pas compliqué de ramer. Passons... Comme personne n'était là pour les accueillir, ils n'étaient pas encore au courant de leur mort et que les esclaves ne devaient plus rien aux maitres. Ils étaient un peu perdus de se retrouver ici, ils comprirent qu'il fallait aller en face mais les maitres commencèrent à douter de la soumission de leur esclave. Ils décidèrent de procéder de telle manière qu'à aucun moment les maitres ne soient en infériorité numérique peu importe la rive. De même, aucun maitre n'acceptera d'être conduit par l'esclave sachant ramer. Ils sont sortis avec un plan, c'était aberrant. Comme je n'étais pas là, la barque pouvait contenir jusqu'à deux personnes. Sauf que ,comme je le rappelle, seulement deux personnes, un maitre et un esclave, savaient conduire la barque. Cela leur a pris je ne sais plus combien de traversées mais ce fut tout un bazar.
- Boarf, on peut facilement trouver, compte tenu de ses contraintes, le nombre minimum de traversées nécessaires." Saurez-vous le trouver?

"En outre, il y avait le grave problème qu'il pouvait revenir du côté initial de la traversée alors que c'est censé être un voyage à sens unique. Bien que Cerbère guette, je me suis proposé à Hadès et me voilà nocher de cette barque.
- Je vois. En parlant de voyage à sens unique et tout ça...hum, vous avez dit tout à l'heure que c'était généralement éternel...Généralement. Cela signifie qu'il y a un moyen de sortir, non?
- Ha...Tu te lance dans une vaine quête. Bon nombres ont essayé et bon nombre ont échoué à de rares exceptions. Le seul moyen "légal" de sortir d'ici est de monter aux Champs Élysées et de boire le Léthé. Celui-ci te fera perdre la mémoire et te ramènera dans le monde des vivants sous une nouvelle forme. Sinon, il va falloir forcer le passage à la porte des enfers. Il te faudra déjà la trouver, passer les pièges qui l'entoure et affronter Cerbère, un horrible chien géant à trois tête.
- Et comment pourrais-je aller aux Champs Élysées?
- C'est aux juges de t'en juger digne.
- Je vois... Et le cas échéants, cette porte des Enfers, comment la reconnaitrai-je?
- Ha ha ha. Tu as vraiment de l'espoir, mon gars. Fait gaffe car c'est ce qui risque de te détruire. On arrive bientôt mais bon, je veux bien t'aider. Aux confins du Pré de l’Asphodèle, tu trouveras non pas une mais 9 portes avec chacun des instructions gravées dessus. Une seule mène hors d'ici. Les instructions de celle-ci sont forcément vrais. Le reste des portes se compose de porte vide, qui t'amèneront simplement là où tu es, au Pré de l’Asphodèle, d'autres par contre t'amèneront direct au Tartare, l'endroit le plus profond des enfers. Si tu souhaites vraiment partir, il va falloir prendre le risque de tomber au pays des supplices et crois-moi, tu n'as vraiment pas envie d'y aller.
- Je m'en moque, continue.
- Comme il te sied. Les portes qui t'amèneront au Tartare auront des instructions forcément fausses. Quant aux portes menant au Pré de l’Asphodèle... à dire vrai, je ne me souviens plus si leurs instructions sont vraies ou fausses.

En 1, tu as "La princesse est dans une cellule dont le numéro est impaire".
En 2, tu as "Cette porte mène au Pré de l’Asphodèle".
En 3, tu as "Les instructions de la 5 sont vraies ou les instructions de la 7 sont fausses".
En 4, tu as "Les instructions de la 1 sont fausses".
En 5, tu as "Les instructions de la porte 2 ou 4 sont vraies".
En 6, tu as "Les instructions de la 3 sont fausses".
En 7, tu as "La sortie n'est pas derrière la porte 1".
En 8, tu as "Cette porte te mènera au Tartare et la porte 9 mène au Pré de l’Asphodèle".
En 9, tu as "Cette porte mène au Tartare et les instructions de la 6 sont fausses"
- Mais attend...Laisse moi réfléchir... Oui, c'est ce qui me semblait, c'est impossible à déterminer la porte qui mène à la sortie.
- Ho, tu as été rapide. Tu es définitivement quelqu'un de spécial. En effet, c'est juste une manière de torturer l'esprit de ceux qui essaient. On ne peut savoir au départ comment sortir. Cependant, j'ai connu un ami qui s'y est risqué. Il a pris la porte 8. Et grâce à son test, je peux te dire si la porte 8 te mène au Pré de l’Asphodèle." Charon lui dit alors et vous sûmes direct quelle porte il fallait prendre.

Vous mettez enfin les pieds sur la terre ferme. Après avoir salué Charon, vous vous enfoncez en ce lieu funeste et désolé. À l'ombre d'un arbre dépourvu de toutes feuilles, vous rencontrez deux enfants qui se chamaillaient. Vous vous permettez de les déranger et de leur demander où vous pouvez trouver le premier juge? "Vous souhaitez rencontrer Minos? s'interrogea l'enfant.
- Pfff, de toute façon, vous serez condamné à rester ici comme la plupart d'entre nous alors à quoi bon? surenchérit l'autre enfant.
- Je souhaite me rendre aux Champs Élysées, répondez-vous.
- Hahahaha, se moquèrent les enfants. Tu ne te prends pas pour un coprolithe, toi.
- Je parie que tu ne serais même pas capable de résoudre une simple énigme, vous nargue l'un.
- Fort bien. Testez moi. Si je réussis, vous m'indiquerez où trouver Minos, les défiez-vous.
- Mmmm...Voyons voir. J'ai la liste suivante:

1) Dans cette liste, il y a exactement 1 phrase fausse
2) Dans cette liste, il y a exactement 2 phrases fausses
3) Dans cette liste, il y a exactement 3 phrases fausses
4) Dans cette liste, il y a exactement 4 phrases fausses
5) Dans cette liste, il y a exactement 5 phrases fausses
6) Dans cette liste, il y a exactement 6 phrases fausses
7) Dans cette liste, il y a exactement 7 phrases fausses
8) Dans cette liste, il y a exactement 8 phrases fausses
9) Dans cette liste, il y a exactement 9 phrases fausses
10) Dans cette liste, il y a exactement 10 phrases fausses

Lesquelles sont vraies, lesquelles sont fausses?

- Mais non, idiot. L'énigme n'est pas avec "exactement" mais avec "au moins", coupa l'autre enfant.
- Ne va pas m'embêter, c'est pareil!
- Vraiment?
- Bah laissons le monsieur voir s'il y a une variation entre l'énoncé avec exactement et au moins. Pour cela, il va évidemment nous dire les bonnes solutions pour les deux cas et on verra bien si c'est pareil. Allez! On vous écoute.

"Très bien, très bien. Nous n'avons qu'une parole. Tu trouveras les juges dans le Champs de la Vérité. Là bas, il n'y a pas d'honnête ou de menteur. Tout le monde est obligé de dire la vérité. Cela doit rendre la tâche des Juges beaucoup plus facile. Surement pour ça qu'ils sont là-bas.
- Sauf si c'est les juges qui ont fait de cet endroit un lieu de vérité, objecta l'autre enfant.
- Oui, pas faux. On sait qui fut là en premier?
- On s'en moque! , coupez-vous. Comment puis-je m'y rendre?
- Calme, tu as toute l'éternité devant toi! C'est tout droit, dans cette direction."

Après avoir saluer les enfants, vous prenez congé en suivant la direction indiquée. Vous arrivez devant un palais dans lequel vous rentrez...Une longue, très longue fil d'attente se profile jusqu'au trône où siège un homme géant, sans doute Minos. Ce dernier était en train de juger une personne. Celle-ci expliqua son cas. "J'étais enfermé sur Terre, dans une prison. Je n'ai commis aucun crime, soyez en assuré. J'ai été avec un ami capturé par un ancien soldat que la guerre a rendu fou. Il nous avait enfermé dans deux cellules séparées, dans des départements distincts dont la distance et les murs nous empêchaient de communiquer l'uns avec l'autre. Mon ami est juste derrière, il vous dira la même chose que moi.
- Cela ne répond pas à la question que je t'ai posé, intervint Minos. Pourquoi considères-tu ta mort comme injuste?
- Car il ne nous a laissé aucune chance. On a tenté de négocier. On lui a proposé de l'or, des biens. Il n'a rien voulu entendre. C'est un déraisonné. Il nous a expliqué toutefois qu'il était magnanime. Tss, tu parles. Il a dit qu'à nous deux, nous voyons tous les arbres du domaine par nos fenêtres et qu'il n'y avait aucun arbre qui était vu par nous deux en même temps. Alors, j'ai regardé par la fenêtre, j'y ai vu 8 arbres.
- Et moi, j'ai fait de même mon seigneur et j'en ai vu 12, enchaîna l'ami.
- Il nous annonça que chaque matin, il allait voir mon ami puis moi-même. Il nous posera alors cette même question "Y a-t-il 18 ou 20 arbres dans le domaine?". On peut lui donner une réponse ou passer. Si on passe tous les deux, il recommencera le jour d'après. Si on lui donne une réponse, soit on a juste et on était libéré sur le champs, soit c'est faux et il nous tuait. Mais c'est injuste votre Honneur. On ne pouvait communiquer, je ne pouvais deviner combien d'arbres voyait mon ami. Comment pourrais-je deviner combien d'arbres y avait-il? Alors...après quelques jours où l'on s'est tu...j'ai tenté ma chance. C'était 50/50 après tout. J'ai dit 18...Et nous voilà!
- Pourtant, ce soldat que vous traitez injustement de fou vous a bel et bien laissé une échappatoire. Vous n'avez juste pas été en mesure de la saisir. Votre stupidité ne rend pas votre mort injuste.
- Comment? Vous prétendez qu'il existe une stratégie qui nous aurait permis de sortir de là-bas vivant? Mais comment messire? Avez vous bien saisi la situation? "

Avant que Minos répond, vous sentez que c'est l'occasion rêver pour vous faire remarquer et peut-être aborder Minos sans avoir à parcourir et attendre cette fil d'attente. Il vous suffisait de répondre à cette pauvre âme avant que Minos eut nécessité à la faire. Alors, voyez-vous une stratégie par laquelle nos deux compères auraient pu se sortir de leur guêpier?

"Intéressant, énonça Minos. Approchez, je vous prie. Comment vous appelez-vous?
- Comment ça "approchez" ?!, s'insurgea un homme dans la queue. Vous savez depuis combien de temps on attend? Et lui, il aurait le droit de gruger tout le monde car il a su trouver la solution à une piètre énigme? C'est inadmissible. C'est de l'abus d'autorité.
- Cette personne m'a montré un trait d'esprit des plus remarquables. Je pense qu'on peut le traiter avec plus d'égards, énonça Minos.
- Vous avez sûrement raison, noble juge. Excusez-moi mon agacement mis sur le coup de mon impatience et de mon ignorance. Je ne savais guère qu'on pouvait gagner des places en témoignant de nos aptitudes. Toutefois, il n'en reste pas moins qu'il n'a résolu qu'une simple énigme. De là, on ne peut admettre qu'il a un intellectuel supérieur. Qu'il résolve mon énigme et je le laisserai passer devant moi. Mais dans le cas contraire, vous devrez reconnaître également mon intellect et devrez donc me laisser passer devant!
- Voilà qui me semble une requête juste, déclara Minos. On vous écoute.
- Voici une énigme de mon pays, le magnifique royaume d'Angleterre. Un professeur écrit 6 mots au tableau :

cat, dog, has, max, dim et tag.

Le professeur choisit aléatoirement un mot et l'écrit sur une feuille de papier. Il découpe alors la feuille en 3 de telle sorte que chaque feuille contiennent une seule lettre du mot choisit. Il donna alors à chacun de ses 3 meilleurs élèves une feuille. Il demanda alors au premier "sais-tu quel mot a été choisi?". Le 1er élève dit "oui". Le professeur se tourne vers le 2nd. Après réflexion, le second dit également "oui". Le professeur se tourne vers le 3ème et celui-ci répond "de même". Alors? Quel mot a choisi le professeur?"

Minos s'écria: "Tu as prouvé une certaine valeur intellectuelle. Dis moi, que souhaites-tu?
- Me rendre aux Champs Élysées! répondez-vous sans hésitation.
- Je vois. Pour cela, il te faudra l'aval des 3 juges. Es-tu prêt à passer mon épreuve?
- Affirmatif!
- Alors écoute. attentivement Tu as un circuit hippique qui a 5 pistes pour les chevaux. Tu as 25 chevaux bénis des dieux qui avanceront toujours à la même vitesse. Chaque cheval a une vitesse qui lui est propre et qui est donc constante grâce à la bénédiction. Ton but est de déterminer qui parmi ces 25 chevaux est le plus rapide, le second plus rapide et enfin le troisième plus rapide. Ma question est alors, quel est le nombre minimum de courses nécessaire sachant que tu n'as ni montre ni papier qui te permettrait d'enregistrer le temps mis par un cheval à parcourir le circuit? Le seul moyen de différencier la vitesse de deux chevaux est donc de les faire courir le long du parcours hippiques. Et tu peux faire courir 5 chevaux en une course. Alors, en combien de course peux-tu faire ce qui t'a été demandé?

"Félicitation, s'écria Minos, tu as su résoudre correctement cette énigme qui n'était pourtant pas des plus faciles.
- Ai-je donc votre aval?
- Pas si vite, jeune homme. Une énigme ne serait suffisant. Cela te permet juste de participer à mon épreuve. Un grand héros de guerre vient de brûler avec toute sa maison suite à un incendie déclenché par ses rivaux. J'aimerai lui apporter la paix, il le mérite. Il pleure d'avoir perdu ses 3 enfants et erre comme une âme en peine. Amène lui le repos et mon aval sera tien".
Vous trouvez sans mal la personne désignée par Minos. Vous cherchez à recueillir des informations sur ses enfants. Il vous dit ceci : "Si tu multiplies leurs ages, tu trouveras 36 et si tu les additionnes, tu obtiendras le nombre de batailles que j'ai gagné". Il vous donne le nombre mais vous n'en avez pas vraiment besoin. "Mais avec ce que tu me donnes, je ne peux déduire l'âge de tes enfants, rétorquez-vous
- Pourtant mon fils aîné pouvait.
- Vraiment? Ha mais bien sûr. Très bien, je vois". Et vous? Voyez-vous quelles sont leurs âges?

La question de l’identité est une des plus anciennes questions que les grands penseurs se posent. Qu’est-ce qui fait ce que nous sommes ? Qu’est-ce qui forge notre identité ? De nombreux théologiens, philosophes, psychologues, sociologues et scientifiques ont tenté d’apporter une réponse à cette question. Ainsi, je n’aurai pas l’outrecuidance de prétendre apporter une réponse ici. Il faut savoir rester humble. Cependant, permettez-moi de partager avec vous ma pensée et mes réflexions.

Avec l’effervescence de l’Intelligence Artificielle, on a pu voir des machines de plus en plus penser et surtout apprendre par elles-mêmes. Bien que nous en soyons encore aux balbutiements, on peut aisément imaginer et conceptualiser une machine qui serait capable d’apprendre seule, de pouvoir se modifier toute seule et de finir par se débrouiller seule, de manière autonome à l’instar de la progression humaine. On naît sans rien connaître puis on apprend, encadré d’abord avec nos parents et l’école, puis seul et enfin, on devient indépendant. Cette IA pourra alors avoir ses propres pensées, ses propres volontés… La question qui se pose derrière est : “Dirons-nous que cette IA a une âme, un esprit ?”. Pour le coup, on l’a créé et donc on connait bien ses constituantes. C’est un ensemble de circuits électroniques et une suite d’espaces mémoires activés ou non formant logiquement une chaîne de 0 et 1. Niveau algorithmique, c’est un réseau de neurones. In fine, sa structure cérébrale n’est pas si éloignée de la nôtre. Aujourd’hui, si nos ordinateurs n’ont pas encore leur conscience, c’est bien car on les bride et car il nous a fallu à nous des années d’apprentissage pour arriver là où on en est alors qu’eux, on ne leur laisse pas. Du coup, toutes les pensées et réflexions de cette IA, son comportement, ses envies, etc., n’est qu’une suite d’états d’un ensemble de neurones. En conséquence, a-t-on fait venir un élément extérieur et spirituel tel que l’âme et l’esprit dans cette machine ? Quand s’est-elle formée ou arrivée ? Il vous appartient de répondre en “votre âme et conscience” à cette question. Si pour vous, une IA répondant à cette description n’a pas d’âme/d’esprit, alors il me semble logique que l’humain n’en ait pas, non plus. Tout ce qu’on ferait, penserait ne serait pas la résultant d’une identité spirituelle mais d’un simple mécanisme encodé dans notre cerveau à l’instar d’une machine dont l’unicité dépendrait purement de sa phase d’apprentissage soit en d’autres termes, de son vécu.

Si vous pensez qu’il y a toutefois quelques choses qui transcendent la mécanique, vous avez surement raison de penser cela. Connaissez-vous le bateau de Thésée ? C’est une expérience de pensée touchant à l’identité justement. Thésée par en bateau combattre le Minotaure. À son retour victorieux, les Athéniens conservèrent le bateau comme une relique. Ils remplacèrent les éléments qui s’usèrent par d’autres éléments identiques. Ainsi, le bateau subsista pendant des siècles et des siècles. Mais vint un temps, à force, où il ne restait plus aucun élément du bateau d’origine de Thésée. Peut-on dire que c’est le même ? Il y a deux positionnements, soit on dit que c’est le même et dans ce cas, il y a bien un élément qui transcenderait le “physique” de l’objet et qui conserverait son identité même si, au bout d’un temps, l’entièreté matériel est différente. Soit on dit que seul le bateau initial est le bateau de Thésée et qu’on l’a souillé jusqu’à ce qu’il disparaisse en l’altérant en changeant les pièces usées. J’ai un problème sur cette dernière partie. Pourquoi ? Notre corps est composé de près de 10 puissance 13 cellules. Or environ 2000 de cellules meurent chaque seconde chez un adulte “moyen”, soit 50/70 milliards de cellules par jour via le mécanisme naturel de l’apoptose. Par conséquent, notre intégrité physique n’est pas assurée. On perd sans cesse des cellules tout comme elles sont remplacées par de nouvelles cellules créées. Si on considère que le seul moi qui existe est celui d’origine et que chaque altération me “détruirait”, alors je n’existe plus depuis un moment. Et pourtant, je considère toujours que le moi enfant est...moi. Il y aurait donc bien quelques choses qui transcendent le matériel.

Nonobstant, est-ce suffisant pour attester l’existence de l’âme ? Je ne pense pas. En effet, même si l’on change chacun des composants de l’élément, on les remplace à l’identique et ont donc la même fonction, le même comportement, le même aspect. Pour reprendre la comparaison avec l’ordinateur, bien que l’on modifie sa RAM, sa carte mère, ses câbles, il n’en reste pas moins que le code, l’algorithme, reste le même. Et ainsi, peu importe le support matériel, il adoptera le même comportement, forgeant ainsi son unité. Peut-on alors considérer que cet algorithme, ce code serait l’esprit ou l’âme de la machine ? Au final, cela serait ce canevas qui ferait notre unicité avec en plus les modifications qui ont été apportées avec notre expérience, notre vécu. On pourra alors se demander s’il n’est pas de même pour l’homme. Nos neurones seront remplacés, toutefois le maillage qu’ils ont formé reste strictement le même. Ainsi peu importe les modifications, notre cerveau reste identique. Nous conservons ainsi ce canevas, et c’est ce qui transcendent le temps.

Pour autant dans cette théorie, rien ne parle encore du domaine spirituel. Existe-t-il donc réellement une entité extérieure, immatérielle, dont le corps ne serait qu’un simple vecteur ? Ces éléments encodés dans notre cerveau ne seraient alors que la manifestation de cette entité. C’est plutôt difficile, voire impossible, de le démontrer. Néanmoins une autre question se pose : avons-nous UNE âme ? Comment peut-on affirmer que nous ne sommes le vecteur que d’une seule entité ? Peut-être que notre corps est utilisé par plusieurs choses. Prenons l’exemple de la toxoplasmose. Pour ceux qui ne le savent pas, la toxoplasmose est une maladie infectieuse parasitaire. Un parasite nommé le toxoplasma gondii ne peut vivre qu'à l'intérieur de cellules d’organismes de sang chaud, en termes scientifiques, on parle d’organismes homéothermes. Ce parasite ne peut vivre que dans des cellules mais surtout, il ne peut se reproduire que dans des cellules de félidés. Le toxoplasma gondii est alors naturellement attiré par toute la famille des félins car ce dernier ne souhaite pas disparaître. Il a alors une stratégie très simple. Il monte jusqu’au cerveau et va se loger dans l’amygdale de l’hôte. L’amygdale est le lieu qui régit la peur et le désir, elle est notamment responsable de la sécrétion de dopamine, l’hormone du plaisir. De nombreux tests et expériences scientifiques ont montré que des rats infectés ne ressentent plus la peur lorsqu’ils sentent de l’urine de chat mais éprouve plutôt un désir sexuel. La souris est alors attirée par le chat. Ainsi le toxoplasma gondii peut alors infecter le chat où il pourra se reproduire. Cette histoire montre à quel point on peut facilement être manipulé par un parasite. Il faut savoir que cette infection ne touche pas simplement les rats. On estime à un tiers de la population mondiale les personnes infectées par le toxoplasma gondii. Ainsi si vous aimez les chats, que vous aimez les dorloter, que vous souhaitez en avoir, demandez-vous : est-ce vraiment vous qui voulez avoir un chat ou est-ce un parasite qui vous fait croire que vous en voulez un ? Est-ce qu’au final, ce désir pour le chat fait partie de notre identité, car après tout c’est un vrai désir, ou bien comme étant extérieur à ce qui peut être potentiellement l’âme ou l’esprit est-il considéré comme un désir étranger ? Mais ceci n’est qu’un exemple. Votre cerveau est composé de deux hémisphères reliés et communiquant via ce qu’on appelle le corps calleux. À une époque, on soignait l’épilepsie en coupant ce corps calleux et on fit plusieurs découvertes. Déjà, l’hémisphère droite gère la partie gauche du corps et vice-versa pour l’hémisphère gauche. Mais surtout, un seul côté du cerveau détient la parole, le gauche. On a pu le tester en demandant à un patient avec le corps calleux coupé de regarder ailleurs. On lui mit un objet (un Rubik’s cube) dans la main gauche. On lui demanda ce qu’il tenait. Il a répondu rien. En effet, il n’a pas de retour de l’hémisphère droit gérant la partie gauche et pour sa main droite, il ne touche rien, donc il n’a rien. Il arrive souvent que les hémisphères ne soient pas d’accord entre eux. Il peut réellement arriver que vous vouliez faire un geste avec une main et une autre doit l’en empêcher. C’est une désynchronisation de vos deux hémisphères qui ne veulent pas la même chose. Bien souvent, on arrive à trouver un compromis mais des rares cas, on peut avoir de tels conflits. Mais dans ces cas-là, où êtes-vous ? Vous êtes le droit ? Le gauche ? Les deux ? Mais comment ne pouvez-vous pas être en accord avec vous-même ?

Avons-nous une âme ? En avons-nous plusieurs ? Comme je l’ai dit, je ne peux répondre à cette question. Je n’ai fait que dérouler mon flot de pensées. Quelle est votre position ?